「ベイズ推論による機械学習」輪読会

第 1 章: 機械学習とベイズ学習

正好 奏斗(@cosnomi)

目次 1

  1. 機械学習って何？
  • 線形回帰
  • 分類
  • その他の機械学習
  1. 確率の基本
  • 確率分布・Bayes の定理
  • 具体例 (2 つの袋の赤玉/白玉)
  • 逐次推論

目次 2

  1. グラフィカルモデル
  2. ベイズ推論の導入
  • 大まかな流れ
    • 線形回帰
    • クラスタリング
  • 意思決定
  • 利点・欠点

機械学習とは

  • データの特徴を抽出する

  • その特徴に基づいて未知の現象に対する予測を行う

  • 「特徴」って何？

    • 例えば「比例関係」「一次関数」など
    • 比例定数や切片を既知のデータから推測
      • このような値をパラメータという
    • 未知のデータ(x)が与えられたら y を予測できる

ここからは具体的な機械学習について見ていきます

  • 1 つ 1 つを詳しく理解する必要は無いと思います
  • 全体を俯瞰するのがこの章の目的

目次 1

  1. 機械学習って何？
  • 線形回帰
  • 分類
  • その他の機械学習
  1. 確率の基本
  • 確率分布・Bayes の定理
  • 具体例 (2 つの袋の赤玉/白玉)
  • 逐次推論

線形回帰とは

  • 回帰(regression): MM 次元の入力x=(x1,...,xM)∈RM\bm{x} = (x_1, ..., x_M) \in \mathbb{R}^Mからy∈Ry\in \mathbb{R}を求めること
  • M=1M=1ならy=wxy=wxとか (y,w,x∈Ry, w, x \in \mathbb{R})
  • 既知のデータとは
    • x\bm{x}もyyも分かっているデータ
  • 未知のデータとは
    • x\bm{x}は分かるが、yyが分からないので予測したい

線形回帰の式

  • 一般化すると、

    y=w1x1+w2x2+⋯+wMxMy=w_1x_1+w_2x_2+\dots+w_Mx_M

  • という式のw=(w1,w2,...,wM)∈RM\bm{w} = (w_1, w_2, ..., w_M) \in \mathbb{R}^Mを既知のデータから求めたい
  • ベクトルで書くと、

    y=wTxy=\bm{w}^T\bm{x}

  • 内積を転置で表していることに注意
    • a⋅b=aTb\bm{a}\cdot \bm{b} = \bm{a}^T\bm{b}

  • しかし既知のデータもすべて綺麗にこの式に従うわけではない

  • 各サンプル(既知のデータのこと)のnn番目について次のような式を考えられる

    yn=wTxn+ϵny_n = \bm{w}^T\bm{x}_n + \epsilon_n

  • ϵ\epsilonがnn番目のサンプルの誤差あるいはノイズを表している

  • 切片は？2 次以上は考えられないの？

    • x=(1,x1,x12,x2,x22,...)\bm{x}=(1, x_1, {x_1}^2, x_2, {x_2}^2,...)などとしてやれば良い
    • これはグラフだと曲線になるけど「線形回帰」という

どうやって w を学習させるの？

  • 詳しくはあとでやりますが…
  • 代表的なのは最小二乗法
    • 既知のデータについて 2 乗誤差が最小になるようなw\bm{w}を求める
    • (しかし、これは「ベイズ的」ではない…)
    • (ベイズ推論はもっと面白い方法で良いw\bm{w}を求める)

目次 1

  1. 機械学習って何？
  • 線形回帰
  • 分類
  • その他の機械学習
  1. 確率の基本
  • 確率分布・Bayes の定理
  • 具体例 (2 つの袋の赤玉/白玉)
  • 逐次推論

回帰から分類へ

  • 分類(classification)も機械学習においてよく出てくるタスク
    • y∈{0,1}y \in \{0, 1\}のように離散的な値を取る
    • 例えば 0 が陰性、1 が陽性みたいな
    • 多クラス(0: 陰性, 1: 軽症, 2: 重症みたいな)は後で
  • 線形回帰では連続値yyを予測した
    • 離散的な値はどう予測する？

連続値を確率とみなす

  • 回帰で求めた値(μn\mu_nとします)は実数全体を取りうるのでややこしい
  • f:R→(0,1)f: \mathbb{R} \rightarrow (0,1)みたいな関数によってμn\mu_nを(0,1)(0,1)に移せれば簡単
  • μ\muを「クラス 1 に分類される確率」として考えられる
    • f(μ)≥0.5f(\mu)\geq 0.5ならyn=1y_n=1、そうでないならyn=0y_n=0とすればよい
  • どんな関数が良いだろう…

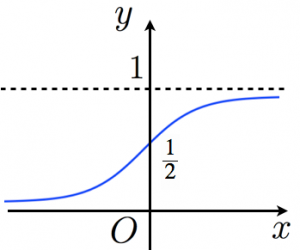
Sigmoid function

  • 有名な関数: シグモイド関数(sigmoid function)

    Sig(a)=11+e−a\mathrm{Sig}(a) = \frac{1}{1+e^{-a}}

  • σ(a)\sigma(a)とか表記されることもある

center

ここまでを数式でまとめる

  • 今やりたいのは
    • 入力xn=(x1,x2,...xM)\bm{x}_n=(x_1, x_2, ... x_M)が与えられて
    • 出力yn∈{0,1}y_n \in \{0, 1\}を求めたい
  • 線形回帰によりμn\mu_nを求める

    μn=wTxn\mu_n = \bm{w}^T\bm{x_n}

  • 既知のデータから良い感じのw\bm{w}を求めて、未知のデータにも適用
  • Sig(μn)\mathrm{Sig}(\mu_n)をとって、0.5 以上なら 1、そうでないなら 0

多クラス分類

  • 0: 陰性, 1: 軽症, 2: 重症 みたいな分類をしたい
  • 非医学で言えば、手書き数字の認識(MNIST)などが有名
  • 各クラスごとの確率を出す
    • 先ほどの例では、最終的な出力は「クラス 1 に分類される確率」
    • k クラス分類では出力をkk次元として、i(1≤i≤k)i (1 \leq i \leq k)番目の成分が「クラスiiに分類される確率」を表すことにする
    • 「ことにする」 = そのようにモデルを train する

softmax 関数

fk(a)=SMk(a)=eak∑i=1Keaif_k(\bm{a}) = \mathrm{SM}_k(\bm{a}) = \frac{e^{a_k}}{\sum^K_{i=1} e^{a_i}}

  • この f を softmax 関数という
  • a∈RK\bm{a} \in \mathbb{R}^Kが線形回帰の出力で、fk(a)f_k(\bm{a})はその値から、kk番目のクラスの確率を表す値を求める関数
  • kk について総和を取ると 1 になる (確率として都合の良い性質)
  • sigmoid 関数の拡張
    • 2 変数の場合について softmax を計算して、式変形によって sigmoid 関数の形にしてみると分かる

フォローしてますか？

  • この章では全てを理解する必要はありませんが、
  • なにか質問があればお願いします。


  • ここからは定性的なざっくりとした話が続きます

目次 1

  1. 機械学習って何？
  • 線形回帰
  • 分類
  • その他の機械学習
  1. 確率の基本
  • 確率分布・Bayes の定理
  • 具体例 (2 つの袋の赤玉/白玉)
  • 逐次推論

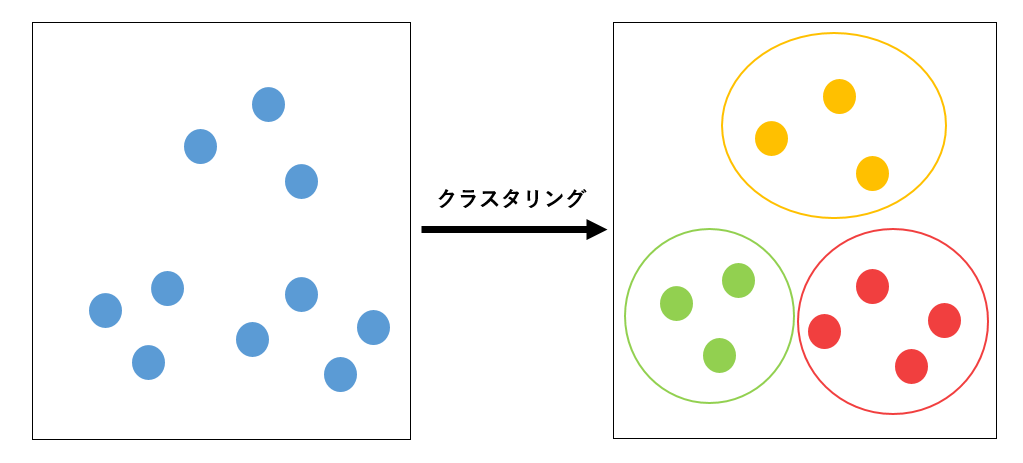
クラスタリング

  • N 個のデータを K 個の集合に分ける
  • 今までの分類タスクとの違いは？
    • クラスタリングは事前の学習をせず、いきなり未知のデータが与えられてそれを良い感じに分ける(教師なし学習)

h:300px center

線形次元削減 (動機)

  • データが増えれば増えるほどより良い予測ができる？？
    • 次元が増えるほど学習が難しくなる (次元の呪い)
  • 次元を減らしたい
    • けど、重要なデータを削ったらもちろん精度は落ちてしまう

つまり…

  • 次元の重要度が高いものは残したい、低いものは消し去りたい
    • 高血圧のリスク予測に「塩分摂取量」は大事そうだけど、「使っている鉛筆の硬度」を入れても精度は上がらなそう

線形次元削減

元のデータY∈RD×N\bm{Y} \in \mathbb{R}^{D\times N} を重みW∈RM×D\bm{W}\in \mathbb{R}^{M\times D}と削減したデータX∈RM×N(M<D)\bm{X} \in \mathbb{R}^{M\times N} (M < D)を用いて近似したい

Y≈WTX\bm{Y} \approx \bm{W}^T\bm{X}

  • X\bm{X}ではなくY\bm{Y}が元のデータ(既知)ということに注意が必要
  • X\bm{X}はY\bm{Y}に含まれるデータの本質を抽出
  • 線形回帰と式が似ている
  • 注意: Y\bm{Y}の特徴量から重要なのを「選び取っている」のではなく、新しい特徴量を作っている

どうやってW\bm{W}を求めるの？

  • Y\bm{Y}とWTX\bm{W}^T\bm{X}の誤差が最小になるようにとか
  • ベイズ的な方法とか
  • 詳しくは後の章で

他にもいろいろ機械学習 (余談)

  • おすすめ商品
  • 自動で質問に答える
  • 人工的に画像を作り出す

などなど

機械学習の 2 つのアプローチ

  • ツールボックス
    • 様々なアルゴリズムを試して性能を高めようとする
  • モデリング
    • データの仮定・制約から数理的なモデルを構築 (モデリング)
      • このデータは正規分布に従うとか、ポアソン分布に従うとか
    • そのモデルのパラメータを推論によって求める (推論)
      • 正規分布なら平均・標準偏差
  • ディープラーニングではツールボックス型が多いが、この本ではモデリングを扱う

目次 1

  1. 機械学習って何？
  • 線形回帰
  • 分類
  • その他の機械学習
  1. 確率の基本
  • 確率分布・Bayes の定理
  • 具体例 (2 つの袋の赤玉/白玉)
  • 逐次推論

確率の基本

  • いよいよ確率の基本に入っていきます
  • 1 年生の頃にやっていたことなのですが、当然、忘れているので適宜復習しながら進めていきましょう。

離散と連続

  • 離散: -3, 0, 1, 4,のように飛び飛びの値
  • 連続: 実数全体を取る。0 と 1 の間にも無数の値が存在する

記法の復習

  • P(X=x)P(X=x): 確率変数XXがxxに等しくなる確率
  • P(X≤x)P(X\leq x): 確率変数XXがxx以下になる確率
  • P(X=x,Y=y)P(X=x, Y=y): 「確率変数XXがxxに等しく かつ 確率変数YYがyyに等しい」確率
  • P(X=x∣Y=y)P(X=x|Y=y):「確率変数YYはyyに等しい」ということが分かっている状況下での確率変数XXがxxに等しい確率

目次 1

  1. 機械学習って何？
  • 線形回帰
  • 分類
  • その他の機械学習
  1. 確率の基本
  • 確率分布・Bayes の定理
  • 具体例 (2 つの袋の赤玉/白玉)
  • 逐次推論

離散確率分布を表す確率質量関数

  • 簡単に言うと、p(x)p(x)はP(X=x)P(X=x)を表す
  • 性質(?)
    • p(x)≥0p(\bm{x}) \geq 0
    • ∑xp(x)=∑x1⋯∑xMp(x1,...,xM)=1\sum_{\bm{x}} p(\bm{x}) = \sum_{x_1} \cdots \sum_{x_M} p(x_1, ..., x_M) = 1
  • 逆にこれらの性質を満たすものを確率質量関数と定義する (後に出てくる連続型分布と対応させるため)

連続型確率分布(確率密度関数)

定義
関数p:x∈RM→Rp: \bm{x} \in \mathbb{R}^M \rightarrow \mathbb{R}で、p(x)≥0p(\bm{x}) \geq 0かつ

p(x)dx=∫⋯∫p(x1,⋯xM)dx1⋯dxM=1p(x) dx = \int \cdots \int p(x_1, \cdots x_M) dx_1\cdots dx_M = 1

となるもの

  • 確率なんだから 0 以上で、全ての場合を足したら 1 になるべき
  • 連続なので難しいけど、x\bm{x}がちょうどその値を取ったときの確率

確率密度関数(1 変数関数の場合)

  • 1 変数は去年?やった

    P(X≤x)=∫−∞xp(t)dtP(X \leq x) = \int_{-\infty}^x p(t) dt

  • 多変数でも雰囲気は同じ

  • 勘違い

    • p(t)p(t)はP(X=t)P(X=t)と同じだ！→ 違います
    • 連続値なので面積で考える。ある 1 点のみの値はあまり確率的な意味合いを持たない

連続と離散をあわせて考える

結局、離散型確率分布の確率質量関数は、連続型確率分布の確率密度関数の積分(連続的な和)をシグマ(離散的な和)に変えただけです。

よって、今後の議論では積分を用いて連続型確率分布について考えますが、同様の議論が離散型確率分布にも適当可能です。

同時分布

  • 2 つの変数x,yx, yに対応する確率分布

    P(x≤X,y≤Y)=∫−∞x∫−∞yp(s,t)dtdsP(x \leq X, y \leq Y) = \int_{-\infty}^{x} \int_{-\infty}^{y} p(s, t) dt ds

周辺化

  • 周辺化: 一方の変数を除去する

    p(y)=∫−∞∞p(x,y)dxp(y) = \int_{-\infty}^{\infty} p(x,y) dx

    • x かつ y の確率が全ての x, y について分かっている条件下で
    • Y=yY=yの確率を知りたいなら、全てのxxについて、それらを足し合わせれば良い
  • このp(y)p(y)を周辺分布という

条件付き分布

  • p(x∣y)p(x|y)のこと

    p(x∣y)=p(x,y)p(y)p(x|y) = \frac{p(x,y)}{p(y)}

  • これはxxについての確率分布である
    • yyの情報はパラメータとして作用し、xxの分布の特性を決める
    • 詳しくは先でやりますが、「既知のデータ y が与えられたら、x の分布は元のp(x)p(x)からより妥当なp(x∣y)p(x|y)に更新される」みたいな感じ

Bayes の定理

p(x∣y)=p(y∣x)p(x)p(y)p(x|y) = \frac{p(y|x)p(x)}{p(y)}

  • p(y)p(y)を両辺に掛ければ両辺がp(x,y)p(x,y)で等しくなる
  • この式自体は割と当たり前のことを言ってるだけ
  • しかし、ベイズ推論ではp(x∣y)p(x|y)をp(y∣x)p(y|x)を使って表したいことが頻発するのでそういう意味で重要

独立性

  • 「x と y が独立である」とは

    p(x,y)=p(x)p(y)p(x,y) = p(x)p(y)

  • あるいは、

    p(x∣y)=p(x)p(x|y) = p(x)

  • すなわち、yyの情報が加わっても役に立たないということ

目次 1

  1. 機械学習って何？
  • 線形回帰
  • 分類
  • その他の機械学習
  1. 確率の基本
  • 確率分布・Bayes の定理
  • 具体例 (2 つの袋の赤玉/白玉)
  • 逐次推論

問題設定

状況: 2 つの袋 a, b があり、それぞれに赤と白の玉が入っている

  • a には赤 2 コ, 白 1 コ

  • b には赤 1 コ, 白 3 コ

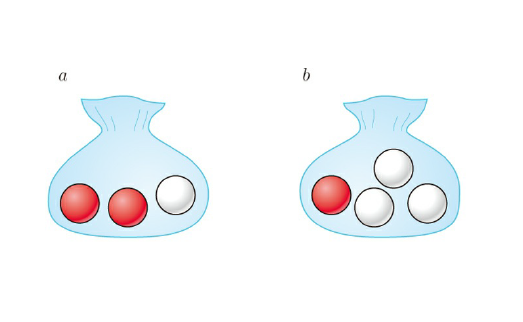
    操作:

  • まず 1/2 の確率で a, b の袋を選ぶ

  • その後にその袋から玉を取り出す

袋の選択

  • 袋 a が選ばれることをx=ax=a, 袋 b が選ばれることをx=bx=bとすると、

    p(x=a)=12,p(x=b)=12p(x=a) = \frac{1}{2}, p(x=b) = \frac{1}{2}

赤白玉の選択

  • 赤玉が取り出されることをy=ry=r, 白玉をy=wy=w
  • 袋 a が選ばれたとき、
    • p(y=r∣x=a)=2/3p(y=r | x=a) = 2/3
    • p(y=w∣x=a)=1/3p(y=w | x=a) = 1/3
  • 袋 b が選ばれたとき、
    • p(y=r∣x=b)=1/4p(y=r | x=b) = 1/4
    • p(y=w∣x=b)=3/4p(y=w | x=b) = 3/4

同時分布を求める

p(x,y)=p(y∣x)p(x)p(x, y) = p(y|x)p(x)が使える
袋 a を選択し、かつ、赤玉を取り出す確率は、

p(x=a,y=r)=p(y=r∣x=a)p(x=a)=14×12=18\begin{aligned}p(x=a, y=r) &= p(y=r | x=a)p(x=a) \\ &= \frac{1}{4} \times \frac{1}{2} = \frac{1}{8}\end{aligned}

  • これを求めること自体は簡単だと思いますが、今回の内容である「同時分布」「条件付き分布」といった概念と関連付けていきましょう！

周辺分布を求める

  • 周辺分布？→p(x,y)p(x,y)をすべてのxxについて足し合わせてp(y)p(y)に
  • 「選んだ袋に関わらず赤 or 白玉が出る確率」を求めることに相当

    p(y=r)=∑xp(y=r,x)=1/3+1/8=11/24p(y=r) = \sum_x p(y=r, x) = 1/3+1/8=11/24

  • 離散なのでシグマを使ったが、連続なら∫\intを使う
  • p(y=r,x)p(y=r, x)はp(y=r,x=x)p(y=r, x=x)と考えると分かりやすいかも

Bayes の定理を使う

メインテーマ！

  • Bayes の定理はp(y∣x)p(y|x)をp(x∣y)p(x|y)を用いて表せる
  • 取り出した玉が分かっているとき、それを袋 a または b から取り出した確率を求められる

    p(x=a∣y=r)=p(y=r∣x=a)p(x=a)p(y=r)=8/11p(x=a|y=r) = \frac{p(y=r|x=a)p(x=a)}{p(y=r)} = 8/11

  • 本当は袋を選んでから玉を取り出したのに、玉が先に分かっていて袋の確率を求めている → 時間を逆行している

事前分布と事後分布

  • 原因(選んだ袋)→ 結果(取り出した玉)
  • Bayes の定理より、結果から原因の確率を計算できた
    • 事後分布: 結果が観測された後の分布 p(x∣y)p(x|y)
    • 事前分布: 結果が観測される前の分布 p(x)p(x)
  • 事前分布にトレーニングデータを与えて事後分布を求める

目次 1

  1. 機械学習って何？
  • 線形回帰
  • 分類
  • その他の機械学習
  1. 確率の基本
  • 確率分布・Bayes の定理
  • 具体例 (2 つの袋の赤玉/白玉)
  • 逐次推論

もっと多くの玉を取り出してみよう(1)

  • 袋 a/b がわからない状態で、玉を取り出し、その結果から袋 a/b それぞれの確率を推定した
  • 複数回取り出して戻す(復元抽出)すれば、より確からしい推論ができそう
  • {y1,y2,y3}={r,r,w}\{y_1, y_2, y_3\} = \{r, r, w\}という結果が得られたとする
  • 求めたいのは、p(x∣y1=r,y2=r,y3=w)p(x|y_1=r, y_2=r, y_3=w)
  • 復元抽出は独立なので、

    p(y1=r,y2=r,y3=w∣x)=p(y1=r∣x)p(y2=r∣x)p(y3=w∣x)p(y_1=r, y_2=r, y_3=w|x) = p(y_1=r|x)p(y_2=r|x)p(y_3=w|x)

もっと多くの玉を取り出してみよう(2)

  • Bayes の定理より

    p(x∣y1=r,y2=r,y3=w)=p(y1=r,y2=r,y3=w∣x)p(x)p(y1=r,y2=r,y3=w)=p(y1=r∣x)p(y2=r∣x)p(y3=w∣x)p(x)p(y1=r,y2=r,y3=w)\begin{aligned}p(x|y_1=r, y_2=r, y_3=w) &= \frac{p(y_1=r, y_2=r, y_3=w|x)p(x)}{p(y_1=r, y_2=r, y_3=w)} \\ &= \frac{p(y_1=r|x)p(y_2=r|x)p(y_3=w|x)p(x)}{p(y_1=r, y_2=r, y_3=w)}\end{aligned}

  • ここで分母の計算が面倒 (周辺化を行う必要がある)

  • p(x∣y1=r,y2=r,y3=w)p(x|y_1=r, y_2=r, y_3=w)はxxのすべての場合について足し合わせると 1 になるので、分子のみを計算して後で合計が 1 になるように調整する ← 今後、頻出するテクです

もっと多くの玉を取り出してみよう(3)

  • x=ax=aについて

    p(x=a∣y1=r,y2=r,y3=w)∝p(y1=r∣x=a)p(y2=r∣x=a)p(y3=w∣x=a)p(x=a)p(x=a|y_1=r, y_2=r, y_3=w) \propto p(y_1=r|x=a)p(y_2=r|x=a)p(y_3=w|x=a)p(x=a)

  • ∝\proptoは比例するという意味。分母を省略しているため。
  • 計算略: x=ax=aについては、2/272/27, x=bx=bについて3/1283/128を得ます。(式(1.42), (1.43))
  • 足して 1 になるように正規化する

    p(x=a∣y1=r,y2=r,y3=w)=2/272/27+3/128=256337p(x=a|y_1=r, y_2=r, y_3=w) =\frac{2/27}{2/27+3/128}=\frac{256}{337}

逐次推論

このように複数の独立なデータがあれば、より確からしい推論を逐次的に行える。

  • 1 つの観測値y1y_1を得たとする。事後分布は、

    p(x∣y1)∝p(y1∣x)p(x)p(x|y_1)\propto p(y_1|x)p(x)

  • さらにもう 1 つy2y_2を得たとする

    p(x∣y1,y2)∝p(y1,y2∣x)p(x)=p(y2∣x)p(y1∣x)p(x)∝p(y2∣x)p(x∣y1)\begin{aligned}p(x|y_1, y_2) &\propto p(y_1, y_2 | x)p(x) \\ &= p(y_2 | x)p(y_1|x)p(x) \\ &\propto p(y_2|x)p(x|y_1)\end{aligned}

目次 2

  1. グラフィカルモデル
  2. ベイズ推論の導入
  • 大まかな流れ
    • 線形回帰
    • クラスタリング
  • 意思決定
  • 利点・欠点

グラフィカルモデル

  • モデルに出てくる変数を視覚的に理解したい
    • 数式だと条件付き分布やその積がたくさん出てきて大変
  • 例えば先程の例だとp(x,y)=p(y∣x)p(x)p(x,y) = p(y|x)p(x)
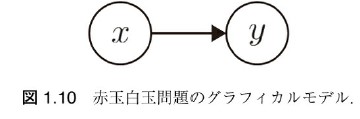
    center
  • 各変数(x, y)が頂点になっている
  • 辺(矢印)は条件付き分布を表す
    • y の分布は x に依存している
  • グラフの構造は DAG(有向非巡回グラフ): 向きがあってループなし

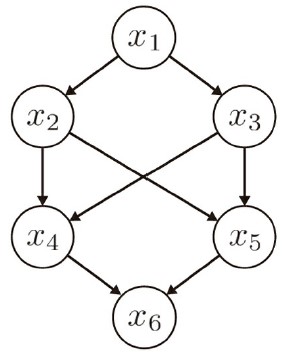
例

p(x1,x2,x3,x4,x5,x6)=p(x2∣x1)p(x3∣x1)p(x4∣x2,x3)p(x5∣x2,x3)p(x6∣x4,x5)p(x_1,x_2,x_3,x_4,x_5,x_6) = p(x_2|x_1)p(x_3|x_1)p(x_4|x_2, x_3)p(x_5|x_2, x_3)p(x_6|x_4, x_5)

  • グラフィカルモデル (ループが存在しないことも注意)
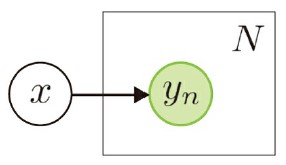
    center

繰り返し(プレート表現)

  • n 個の変数が存在するときなどに使える
  • 先程の逐次推論の例では、N 回の復元抽出を行った。その全ては「袋の選択」x に依存していた。
    center

いろいろなグラフィカルモデル

  • 条件付き分布の関係を視覚的に表現する道具を手に入れた
  • 条件付けのタイプをグラフィカルモデルとともに見ていく
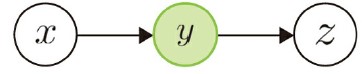
    • head-to-tail
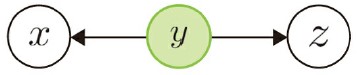
    • tail-to-tail
    • head-to-head
  • yyが観測されているとして、xxやzzの事後分布を考える

head-to-tail

center

  • 式はp(x,y,z)=p(x)p(y∣x)p(z∣y)p(x,y,z) = p(x)p(y|x)p(z|y)
    事後分布は？

    p(x,z∣y)=p(x,y,z)p(y)=p(x∣y)p(z∣y)\begin{aligned}p(x,z|y) &= \frac{p(x,y,z)}{p(y)} &= p(x|y)p(z|y)\end{aligned}

  • もともと xx と zz の間にあった関係は yy が与えられたことで消えて、xx と zz は独立になった

    • 事後分布が独立に分解できる →条件付き独立性

tail-to-tail

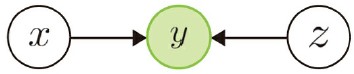
center

  • 式はp(x,y,z)=p(x∣y)p(y)p(z∣y)p(x,y,z) = p(x|y)p(y)p(z|y)
    事後分布は？

    p(x,z∣y)=p(x,y,z)p(y)=p(x∣y)p(z∣y)\begin{aligned}p(x,z|y) &= \frac{p(x,y,z)}{p(y)} &= p(x|y)p(z|y)\end{aligned}

  • xx と yy は条件付き独立

head-to-head

center

  • 式はp(x,y,z)=p(x)p(y∣x,z)p(z)p(x,y,z) = p(x)p(y|x,z)p(z)
  • もともと xx と zz は独立
  • 事後分布は？

    p(x,z∣y)=p(x,y,z)p(y)=p(x)p(y∣x,z)p(z)p(y)\begin{aligned}p(x,z|y) &= \frac{p(x,y,z)}{p(y)} &= \frac{p(x)p(y|x,z)p(z)}{p(y)} \end{aligned}

  • 条件付き独立にならない
    • yyの観測によって、xxとzzに依存関係が生じてしまった

マルコフブランケット

TODO: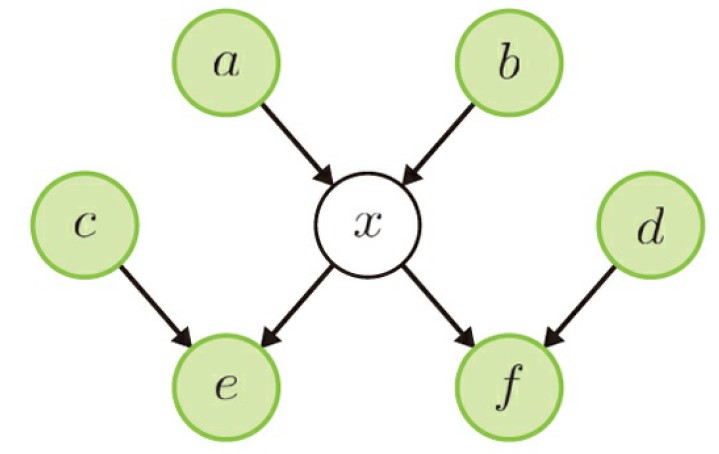

目次 2

  1. グラフィカルモデル
  2. ベイズ推論の導入
  • 大まかな流れ
    • 線形回帰
    • クラスタリング
  • 意思決定
  • 利点・欠点

ベイズ学習の基本

  1. 観測データDDと未知の変数X\bm{X}に関して同時分布p(D,X)p(D,\bm{X})を構築
    • X\bm{X}はモデルパラメータ
    • 例えばDDに正規分布を仮定したなら、X\bm{X}は(m,σ)(m, \sigma)とか
  2. 事後分布の計算

    p(X∣D)=p(D∣X)p(X)p(D)p(X|D) = \frac{p(D|X)p(X)}{p(D)}

    • これは解析的に求められることもあるし、近似的に求めることも
    • p(D)p(D)の計算が難しい (X について周辺化しなければならない)

目次 2

  1. グラフィカルモデル
  2. ベイズ推論の導入
  • 大まかな流れ
    • 線形回帰
    • クラスタリング
  • 意思決定
  • 利点・欠点

線形回帰でベイズを使ってみよう

  • 具体的に「正規分布が～」などの話は抜きにして概略のみ
  • 復習: yn=wTxn+bny_n = \bm{w}^T\bm{x}_n + \bm{b}_n
  • 今は、「サンプルごとのxn\bm{x}_nと共通のw\bm{w}でサンプルごとのyny_nが決まる」ことが大事
  • 「誤差が正規分布に従うと仮定してー」などの話は具体的な分布について扱ってからの話

step1: 同時分布を構築する

P(Y,X,w)=p(w)∏n=1Np(yn∣xn,w)p(xn)P(\bm{Y}, \bm{X}, \bm{w}) = p(\bm{w}) \prod_{n=1}^N p(y_n|\bm{x}_n, \bm{w})p(\bm{x}_n)

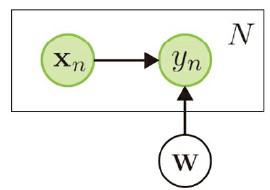
center

  • Y\bm{Y}やX\bm{X}はNN個のサンプルをまとめた行列

事後分布を求める

p(w∣Y,X)=p(Y,X∣w)p(w)p(Y,X)=p(Y∣X,w)p(X)p(w)p(Y∣X)p(X)∝p(w)∏n=1Np(yn∣xn,w)\begin{aligned} p(\bm{w}|\bm{Y}, \bm{X}) &=\frac{p(\bm{Y}, \bm{X}|\bm{w})p(\bm{w})}{p(\bm{Y}, \bm{X})} \\ &= \frac{p(\bm{Y} | \bm{X}, \bm{w})p(\bm{X})p(\bm{w})}{p(\bm{Y}|\bm{X}) p(\bm{X})} \\ &\propto p(\bm{w})\prod_{n=1}^Np(y_n|\bm{x}_n, \bm{w}) \end{aligned}

  • 途中でx\bm{x}とw\bm{w}が独立であることを用いた

未知のデータに対する予測

  • 未知の入力をx∗x_*それに対応する予測出力をy∗y_*とする。

    p(y∗∣x∗,Y,X)=∫p(y∗∣x∗,w)p(w∣Y,X)dwp(y_* | x_*, \bm{Y}, \bm{X}) = \int {p(y_*|x_*, \bm{w})p(\bm{w}|\bm{Y}, \bm{X}) dw}

  • 既知のデータY,X\bm{Y}, \bm{X}を用いて学習されたパラメータw\bm{w}の分布を用いて、未知の入力x∗x_*に対して期待される出力y∗y_*を求める
  • 重要: パラメータwwを 1 つの値に決めるのではなく、その事後分布p(w∣Y,X)p(\bm{w} | \bm{Y}, \bm{X})を求めて(学習して)周辺化するところがベイズ的

目次 2

  1. グラフィカルモデル
  2. ベイズ推論の導入
  • 大まかな流れ
    • 線形回帰
    • クラスタリング
  • 意思決定
  • 利点・欠点

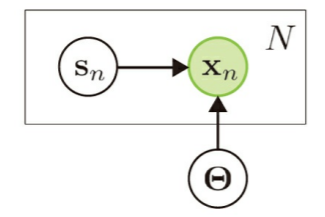
クラスタリング

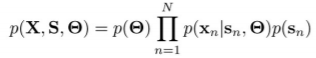
center

  • X={x1,...,xn}\bm{X}=\{\bm{x}_1, ..., \bm{x}_n\}: 観測データ
  • S={s1,...,sn}\bm{S}=\{\bm{s}_1, ..., \bm{s}_n\}: クラスタの割り当て方
  • Θ={θ1 ...,θk}\bm{\Theta}=\{\bm{\theta_1}\, ..., \bm{\theta_k}\}: 各クラスタの性質
    center

近似

  • 事後分布の計算において、周辺化を伴うp(D)p(D)の計算は計算量的に難しい
  • サンプリング
    • MCMC
    • ギブズサンプリング
  • 変分推論

目次 2

  1. グラフィカルモデル
  2. ベイズ推論の導入
  • 大まかな流れ
    • 線形回帰
    • クラスタリング
  • 意思決定
  • 利点・欠点

ベイズ推論の利点

  • 一貫性のあるアプローチ
    • ディープラーニングでは、このタスクにはこっちのモデルがいいけど、別なタスクには応用できないみたいなこともある
  • ドメイン知識の導入が容易
    • 医療者としての知識を確率モデルに反映
  • 過剰適合しにくい
    • 事前分布に強い仮定を置いている
    • 「学習」は分布を更新しているだけ

ベイズ推論の欠点

  • 数学が難しい
    • その分、数学的な根拠がしっかりしている
  • 計算コスト
    • ディープラーニングも大概だけど

第 2 章では…

  • 具体的な確率分布について見ていきます
    • 事後分布や周辺分布の計算を具体的にできるようになります
    • モデル選択は実際にデータ解析を行う上で非常に重要です

相談:

  • 計算多めですが、どの深さまで追うべきでしょうか
  • 担当はどうしますか / LT?
  • 次回日程
  • メンバー

TODO: 余裕があればパラメータ推定の話をここに入れる