平均
- としたときの期待値
- つまり
- 期待値の定義より
-
確かに平均っぽい
-
2 乗の平均に相当する値:
- スカラーで考えると、
分散
- スカラーなら「平均との差(=残差)の 2 乗の平均」であった
- 分散の定義
- 先程の 2 乗の平均に相当する値を思い出す
- が残差なので結局、残差 2 乗平均っぽい
- 2 乗の平均-平均の 2 乗と同じ形
条件付き期待値
- を考えたい
- 独立なら単に分解できて、
- 独立でないとき
- 見た目は怖いけど、よく考えると妥当に見える
- との間には関係がある(← 独立でない)から、外側の<>でを仮定してるのなら、単にではなくを考えてあげないといけない
- を条件付き期待値という
エントロピー
- エントロピーとは確率分布に対して定義される値で、
-
確率分布の「乱雑さ」を表す
- 実は対数が大事なのではなく、で逆数を取っていることが「乱雑さ」を表現している
- は「起こりやすさ」、は「予測しにくさ」という気分
-
定義なので受け入れるしかない…
KL ダイバージェンス
-
2 つの確率分布がどれくらい離れているかを表す値
-
注意:
離散確率分布
- ここから色々な離散確率分布を見ていきます。
- 必要な事前知識はこれだけ
- 離散分布において、はを表す
- すなわち確率変数がである確率
- は「サイコロの目が x である確率」みたいな感じ
- 「定義」「どんな意味を持つか」「期待値などの計算」を抑える
ベルヌーイ分布の定義
- とパラメータを用いて
- この分布の気持ちは簡単
- は必ず 0 と 1 のどちらかを取る値
- となる確率がとなるような分布が欲しい
- 定義の式に x=0 と x=1 を代入してみよう
- 理由: となる確率はなので
- 理由: なので結局変わらない
ベルヌーイ分布のエントロピー
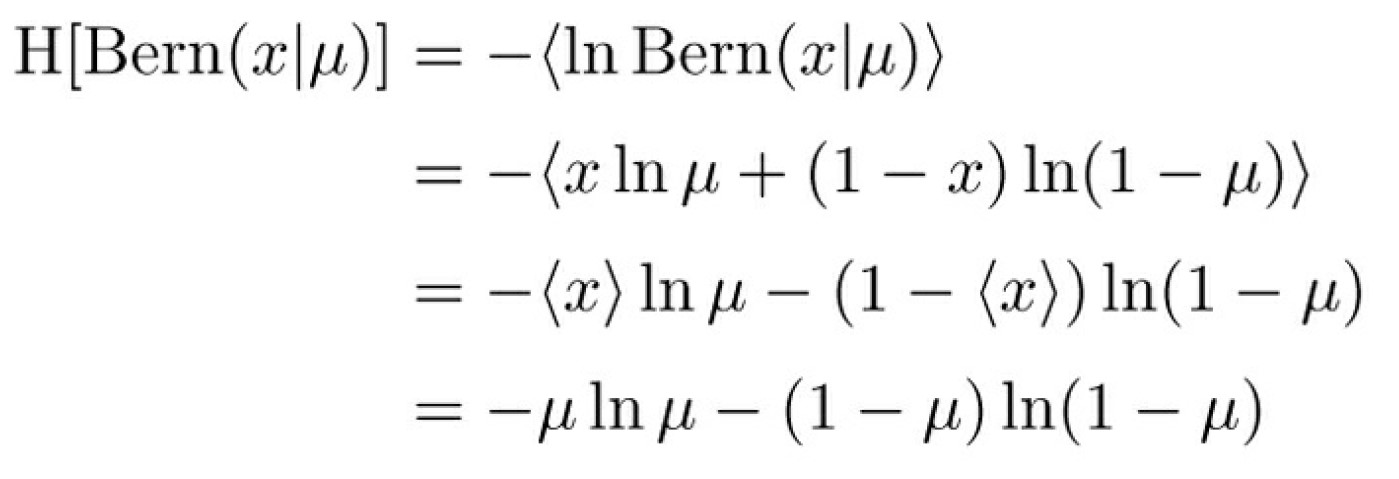
- 定義に従って計算しているだけ
- 確率変数でない定数は外に出せる (とか)
ベルヌーイ分布の KL ダイバージェンス
- パラメータの異なる 2 つのベルヌーイ分布の KL ダイバージェンス
- 単なる計算練習(だと思ってます)
- エントロピーは既に求めているので代入して整理するだけ
- この式ではエントロピーを求めた対象の分布のパラメータがであることに注意
二項分布
- 1 回投げると表がの確率で出るコイン
- 回投げたとき、表が出た回数 の分布を考えたい (ならベルヌーイ分布と同じ)
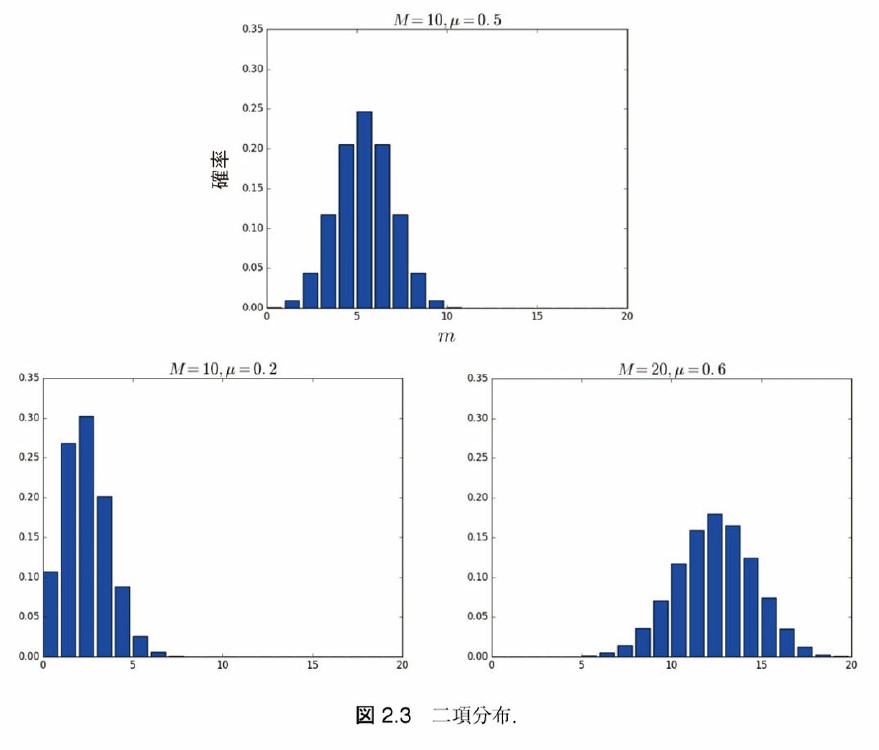
二項分布の形
- 細かい計算はいいとして…形を知っておくことは大事
one-hot 表現
- ここからはコインの表裏のようにではなく、3 つ以上の結果について考えます
- では、とすれば良いでしょうか
- 0,1,2…には大小関係が定義される
- 事象同士に大小関係を考えるべきか?
- 名義尺度: 量的な意味を全く持たない。質的な値。
- それより各事象が 0(起こらない), 1(起こる)を考えたい
- K 個の事象が起こるとき、K 次元ベクトルを考える
- K コの成分のうち1 つだけ 1、それ以外は 0 例)
カテゴリ分布の定義
- ベルヌーイ分布を表裏だけでなく、K 次元に拡張したい
- サイコロなら
- 試行回数は1 回 (二項分布と混同しないで)
-
K 次元ベクトルと、それぞれの事象の確率
-
- 欲しい確率以外は 0 乗されるので影響しない
カテゴリ分布とベルヌーイ分布
- 形が違うように見えるけど…?
- 表 or 裏をカテゴリ分布で考えるとになる
- ベルヌーイ分布では、の確率がなら、の確率は 1 から引くだけ という性質を利用して 2 次元を 1 次元にした
- カテゴリ分布もを利用すれば、K-1 次元に減らせるが、複雑なのでそうしていないだけ
カテゴリ分布の計算
- 今、確率変数にスカラーではなくベクトルを考えているので、期待などもベクトル になるが、各成分について簡単に計算できる
- (結局、各成分は 0or1 だから 2 乗しても同じ)
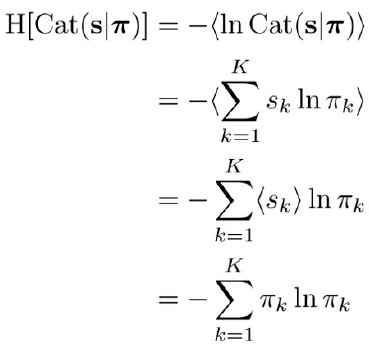
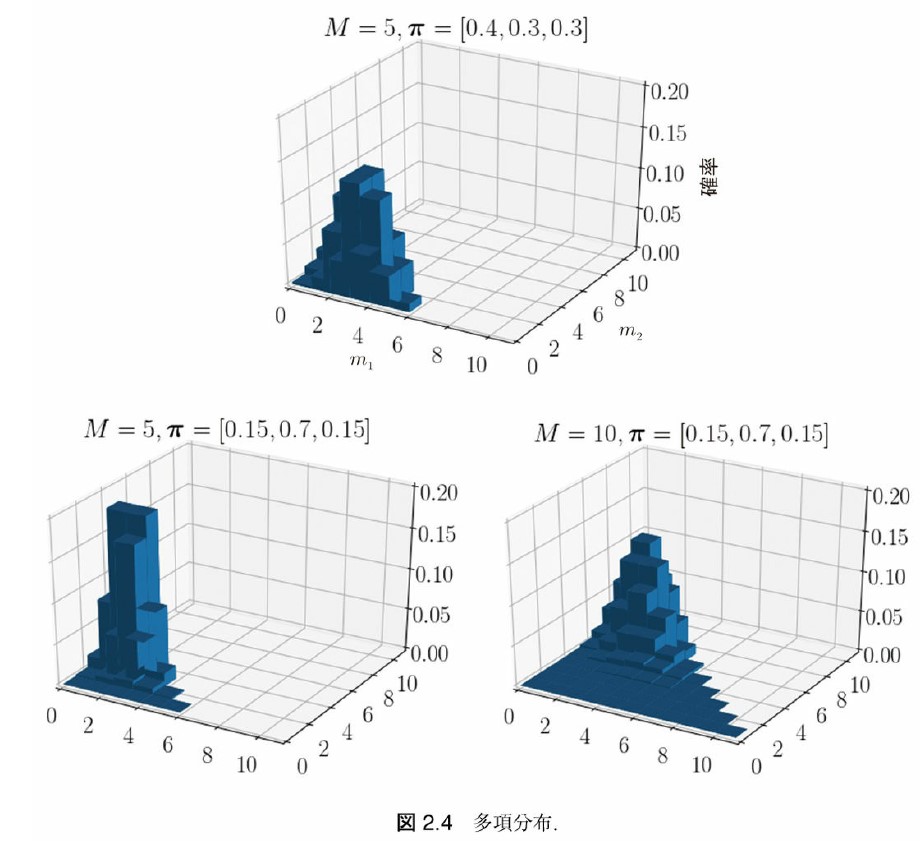
多項分布の気持ち
- 多次元 + 多試行
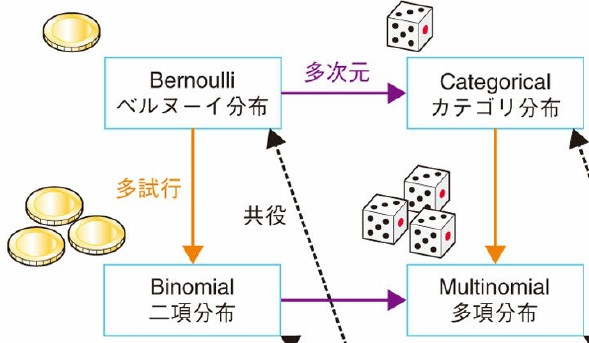
- サイコロ()を回投げたときの目が回出る確率は?
多項分布の定義
- K 個の事象が起こる試行を M 回行う
- は K 次元ベクトルで、k 番目の事象が起こった回数
- は K 次元ベクトルで、1 回の試行で k 番目の事象が起こる確率
- とかとかは「同じものがあるときの順列公式」による
多項分布の形
- がベクトルなのでとしてとのみを表示すると…
多項分布の期待値など
-
「番目の事象」の確率が、「それ以外の事象」の確率が
- 1 成分だけ見るなら、二項分布とみなせる
- 平均・2 乗の平均も二項分布と同じ
多項分布の共分散
- では二項分布ではなく多項分布を考えるメリットは?
- 「それ以外の事象」を細かく分けて調べられる
- とそれ以外、ではなく、とのように
- ()
ポアソン分布
- 今までの分布とは少し別グループの分布
- 正の実数をパラメータにとり、正の実数を生成
- 一定時間で、平均回起こる事象が、同じ時間で回起こる確率
- 二項分布の近似
- 一定時間で ⇔ 一定回数の試行で
- 交通事故の正面衝突は「車がすれ違う」という非常に多く起こる試行に対して、衝突する確率が非常に小さいためにポアソン分布が使える
- とが別々に分かっていなくても積さえ分かっていれば使えるのが便利
- 二項分布の近似
ポアソン分布の期待値など
連続型確率分布
- 今までの離散型確率分布とは大きく変わります
- 分布の意味を考えるのは難しくなるかもしれません
- 分布の形に注目
- その分布がどのような値を生成するのかに注目
- 実数全体?正の実数だけ?
確率密度関数(復習)
- 連続型確率分布においてというのはそれ単体では確率になりません
- 余談: 確率とは → コルモゴロフの公理(0 以上 1 以下、全事象の確率は 1、完全加法的)
- そもそもはに収まるとは限らないので確率ではない
- 積分して初めて意味を持つ
- このが確率密度関数で、と書かれることもある。
分布が値を生成する とは?
- 今までの分布の見方: 「パラメータ(コインの裏が出る確率など)が与えられている。ある確率変数 X(コインの裏の回数とか)が特定の値になる確率をパラメータを用いて表現する。」
- 生成する見方: 「パラメータが与えられている。するとパラメータを用いて確率変数 X が特定の値になる確率を計算できる。その確率に基づいて X を生成できる。」
- 別に何かが変わるわけではなく、見方が異なるだけ
ベータ分布
- パラメータを用いて、を生成する
- は 1 つの関数
- ガンマ関数を組み合わせた関数
- 正直言うとあまり気にしなくて良い
- 「正規化項」だから
- 何それ
正規化項
-
すべての事象の確率の和を 1 にするための係数とか項とか
-
← 確率としてダメ
-
← 全て 2 で割ってあげると確率の公理を満たす
-
正規化項は「確率変数に依存せずパラメータのみに依存する」
- の値によって何を掛けるかが変わったりしない
- ということは、全ての X について密度関数(仮)を計算してから、合計が 1 になるように適当な値を全てにかけてあげればちゃんとした密度関数になる
- 正則化項の値を計算する必要はない
ベータ分布の形
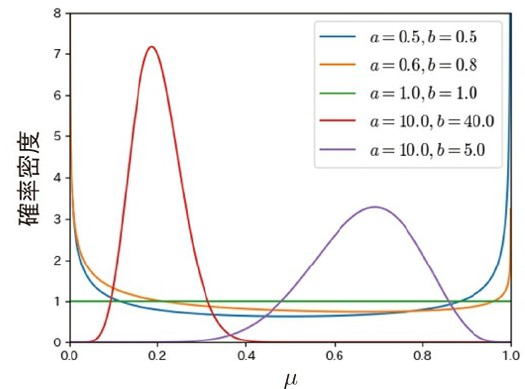
- 2 つの正実数パラメータがあって、の実数を生成します
- 以上!
次の分布は…
- 確率分布の羅列は飽きた、ベイズ推論をさせろ
-
はい…
-
離散型確率分布を一旦飛ばして、これまで学習した分布のみでできるベイズ推論を見ていきます
- この内容は離散型確率分布を全て終えてから、体系的にもう 1 度繰り返すと思います
- 今は、学習した内容がどのように活かされるのかに注目してもらえれば大丈夫です
ベルヌーイ分布に対する推論
- 何をしたい?
- 今、確率変数がある。
- 表裏の出る確率が不明なコインを投げるみたいな感じ
- 便宜上、表を 0、裏を 1 とする
- そして、何回か投げて表か裏かを調べた
- コインの表/裏の取る分布を予測したい
- 今、確率変数がある。
求めたいのは何か、ベイズ推論とは何か?
- コインの表裏が取る分布は「コインの裏が出る確率」を求めて、それをパラメータとするベルヌーイ分布を考えれば良さそう
- 微妙に違う
- 「1 回投げて裏でした → 裏の出る確率は 1 だと思います」
- 本当?でいいの?
- じゃあ分散も一緒に書いてみる?区間推定?
- それも一つの手段だけど…
- ベイズ推論は「コインの裏が出る確率」の分布を求める
たくさん観測すればより確かに
- は一定値ではなく、そのものも確率変数と考える
- 裏が出る確率はコインを投げて観測すればするほどより確かに
- 観測を回行って、裏が出る確率の分布

- 最初は全く見当がついていない
- 少し 0.25 あたりかもと思い始める
- N=50 では、かなり 0.25 っぽいと思っている
x の分布
- まずは「コインを投げて表裏を見る」という事象そのものを考える
- 表を, 裏をとすれば、となるはず
- 裏が出る確率がで、表が出る確率は
- ベルヌーイ分布を仮定できそう
- そしてベイズ推論では、も確率変数と考える
- どのような分布に従うだろうか…
の従う分布(事前分布)
- は裏が出る「確率」なので 0 以上 1 以下だ
- を生成するベータ分布が良さそう (← 開閉の差はあれど)
- は与えられている(=定数)ことにしよう
- 実は、テキトーにを選んでもの分布はそれっぽいものに近づいていくことが知られている
- : パラメータ
- : パラメータのパラメータ: ハイパーパラメータ
分布を整理しよう
-
- は自分で決める、あなたが決める
- は自分で決める、あなたが決める
トレーニングする
- 今、既知のデータがあったら、何が変わるだろう
- つまり、コインを何回か投げて表裏を調べたら、そこから何が分かる?
- パラメータの分布が変わる!
- は、既知のデータを利用することで、より確かな分布となる
- : 事前分布
- : 事後分布
- どのようにを計算すれば良いだろうか…?
事後分布を求める(1)
- ベイズの定理を使う
- 最後はを計算したくないから、分母を無視した
事後分布を求める(2)
- 指数部分が複雑になるので、対数をとってから計算する
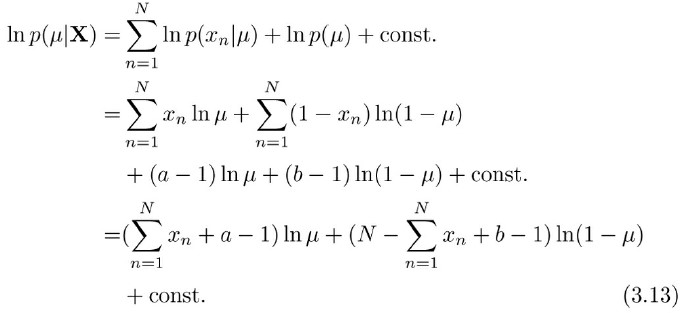
事後分布はパラメータ更新しただけだった
- これって、ベータ分布の対数を取った形では…?
- 事前分布もベータ分布だった。つまり…
- 事後分布は上のようにパラメータを更新したベータ分布になる
予測分布
- 今からコインを投げます。表裏が(=0 or 1)になる確率は、
- 今回は計算を省略しますが、になります
いかがでしたか?
-
細かい計算は思いっきり飛ばしてしまいましたが、何となく、今回学習した分布の式が実際に推論で役に立つことが分かっていただけたら嬉しいです。
-
ベルヌーイ分布だと「ふーん
」って感じだと思いますが、今後、色々な分布を扱えば、もっと面白い事ができます。
- しかし、基本的な流れは今回と同じなのです!
-
次回は飛ばしてしまった連続型確率分布をいくつか扱った後、より体系的に今回のベイズ推論をまとめていきます。